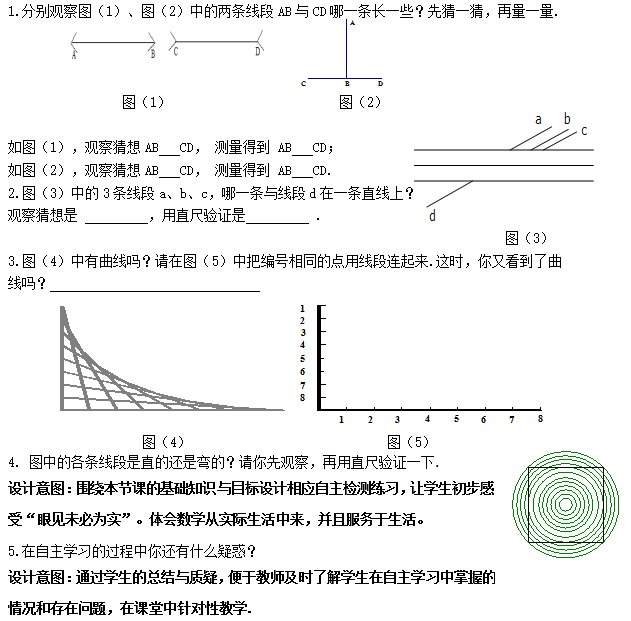
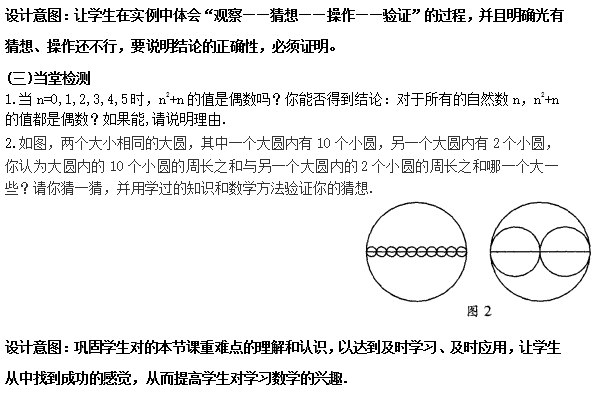
学习目标： 1.经历一些观察、操作活动，并对获得的数学猜想进行试验验证，体验直观判断有时不一定正确，从而尝试从数学的角度运用所学的知识和方法寻求证据、给出证明.2.在交流中，感受数学思考的合理性和严密性.

一、教材地位

《证明》是苏教版八年级下册第十二章《平面图形的认识（二）》的第一节内容。学生经历了小学六年、初中两年来对数学图形感性的、粗线条的认识以及对简单数学问题的合情推理过程学习后，对事物的感性认识并不一定正确的。还需要学习有条理地思考和理性说明问题、并对问题进行演绎推理。而这个过程首先要让学生认识到感性的并不一定是正确的，从而产生新旧知识的冲突，说明演绎证明的必要性。本课主要是让学生通过对生活的体验、数学的观察、计算、操作等途径发现感性认识往往是错误的，只有通过说理、证明等方法才能说明问题的正确性，它是学生从合情推理到演绎推理的必定要思考的问题，是解决下一步“为什么要进行证明？”的关键。在本册书中本课起到高屋建瓴的作用，使下一步的《证明》水到渠成。

二、教学目的

历经综多观察、实践检验，并结合数学思想进行实测验证，直观判断和浅尝辄止的实验操作所获得得感知有时不一定正确。

一、课前自主学习

（一） 教材导读：阅读课本147页至149页，回答下列问题：

1. 无论x取什么数，代数式的值总是正数吗？请你仿照书上的做一做进行说明.

2. 148页数学实验室中活动1的图（2）能实现吗？你有什么看法？请在旁边空白处进行说明.

（二） 方法指导：

从本课的观察、猜想、操作活动中，我们感受到观察、猜想、操作、实验是人们认识事物的重要手段，但是仅凭观察、猜想、操作、实验是不够的，要正确地认识事物，不能单凭直觉，还要学会说理.

（三）课前自主检测：