《 图形的密铺》教学设计
湖塘实验中学 王燕萍
这节课主要是让学生在课堂教学中经历探索多边形密铺条件的过程,从而发展学生的合情推理能力、合作交流意识和一定的审美情趣,进一步体会平面图形在现实生活中的广泛应用性和普遍存在性.基于此,本节课的教学设计,主要采用观察、实际操作、合作设计等各种手段,在借助图形直观进行合情推理的过程中,增强学生的探究好奇心,加深对数学的理解,激发出潜在的创造力,逐步形成创新意识.
学习任务:
(1)经历探索多边形密铺条件的过程,进一步发展学生的合情推理能力.
(2)通过探索平面图形的密铺,知道全等的任意三角形、四边形或边长相等的正六边形及一些正多边形的组合可以密铺,并能运用这几种图形进行简单的密铺设计.
(3)在探索活动中,培养学生的合作交流意识和一定的审美情感,使学生进一步体会平面图形在现实生活中的广泛应用.
(4)在探索性活动中,开发、培养学生的创造性思维,使其理论联系实际.
教学重点:多边形密铺的条件.
教学难点:运用密铺的知识进行图案设计.
课前准备:若干边长相等的正三角形、正方形、正五边形、正六边形以及全等的三角形、全等的四边形的彩色硬纸片及固体胶等.
一.情境引入
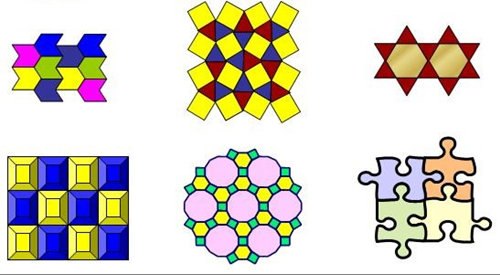
1.上图是一些利用图形的密铺设计而成的图片,请同学们欣赏,并说说每个图案分别是由哪些“基本图形”密铺而成的?
2.揭示平面图形密铺的定义:用形状、大小完全相同的一种或几种平面图形进行拼接,使图形之间没有空隙,也没有重叠地铺成一片,叫做图形的密铺.
点评:学生通过欣赏去感受身边美好的事物,感受数学在生活中的应用.激发学生探究的兴趣.
那么我们今天就来探索平面图形的密铺.
二.探究活动
1.探究用全等的正多边形进行密铺的条件.
(1)学生以学习小组为单位,分别用边长相等的正三角形、正方形、正五边形、正六边形尝试进行密铺;
(2)想一想在铺的过程中要注意什么?
(3)在这些正多边形中,哪些可以进行密铺?哪些不可以?
(4)思考:为什么有的正多边形可以密铺?有的不可以?跟什么有关系?
(5)还有其它边长相等的同一种正多边形可以进行密铺吗?
点评:从全等的正多边形开始,探究平面图形密铺的条件,每一种正多边形的边长都相等,这样学生就不用考虑边了,这就促使学生去关注角.学生通过自己动手操作,合作交流,能够发现:要使边长相同的正多边形能够密铺,只要使拼接点处几个角的和恰为360º.
在边长相等的正三角形、正方形、正五边形、正六边形中能够进行密铺的有正三角形、正方形、正六边形.
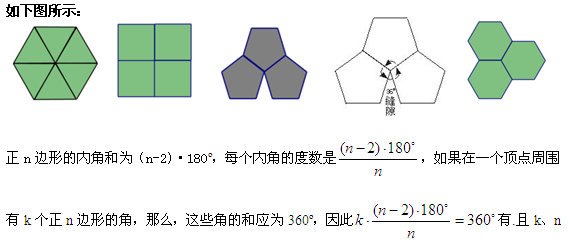
2.探究用全等的一般三角形、四边形能否进行密铺?
(1)学生以学习小组为单位,分别用全等的一般三角形、四边形尝试进行密铺;
(2)在铺的过程中要注意什么?
(3)展示你的成果,说一说你是怎么铺的?
(4)思考:用全等的五边形、六边形…能否进行密铺?
点评:在探究1中,学生已经初步感受到,要使平面图形能够密铺,只要使拼接点处几个角的和恰为360º.而三角形的内角和为180º,四边形的内角和为360º,所以铺的时候要将不同的几个内角拼在同一个顶点处,而且,这里不是所有的边都相等,所以铺的时候要将不同图形中相等的边重合在一起.通过探究2,使学生知道全等的一般三角形、四边形都可以进行密铺,进一步体会平面图形密铺的条件.
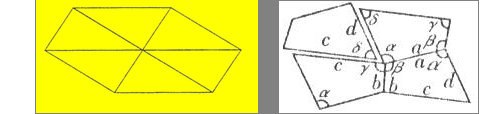
边数多于4的多边形内角和都超过360º,因此只有全等的三角形、四边形能进行密铺.
点评:用探究2获得的知识解决问题:通过关注这些多边形的内角和可以判断全等的一般五边形、六边形…是不能进行密铺的.因此,只有全等的三角形、四边形能进行密铺.
3.探究用边长相等的正多边形材料组合进行密铺的条件.
(1)操作:用边长相等的正三角形、正方形组合能进行密铺吗?
(2)在每一个拼接点处有几个正三角形?几个正方形?请你用一元二次方程的正整数解得有关知识进行解释.
(3)思考用边长相等的正多边形材料组合进行密铺的必要条件是什么?
(4)用边长相等的正三角形、正六边形材料组合能进行密铺吗?如何铺?试说明理由.
(5)思考:用边长相等的正五边形、正十边形材料组合能进行密铺吗?为什么?
点评:进一步熟悉平面图形密铺的条件.要使边长相等的正多边形材料组合能密铺地面,就必须满足这些正多边形的若干个内角能够围绕一点拼成周角.
设在一个顶点周围有m个正三角形的内角和n个正方形的内角,那么这些角的和应满足条件
同样如果是用边长相等的正三角形、正六边形材料组合进行密铺,
这个二元一次方程的正整数解为m=2,n=2或m=4,n=1.

正三角形、正方形组合 正三角形、正六边形组合
对边长相等的正五边形、正十边形组合,围绕一点, 2个正五边形的内角和1个正十边形的内角能拼成周角,但不能扩展到整个平面.如图所示.
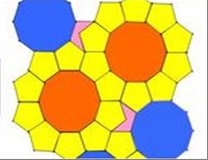
所以,对正多边形的密铺问题,“正多边形的内角能够围绕一点拼成周角”,
只是图形能否密铺的一个必要条件.
三.尝试应用
密铺是丰富多彩的,我们能否用几种边长相等的不同边数的正多边形密铺呢?请你来做一个设计师,动手画出密铺后的图形,并给不同的多边形涂上不同的颜色,设计成漂亮的图案.
点评: 生活中处处存在着数学,数学来源于生活,又服务于生活.数学本身存在美,更能创造美.通过这个环节,进一步体会图形能够密铺的必要条件.同时让学生通过自己动手去创造美,获得成功的体验.
四.总结提升
我们通过活动、探究知道任意一个三角形、四边形或正六边形可以密铺成一个平面,一些边长相等的正多边形组合也可以进行密铺,并探索出正多边形密铺的必要条件,即:正多边形的内角能够围绕一点拼成周角.
五.教学反思
创新,源于“问题”.几何图形的直观形象为学生进行自主探索、创新的活动提供了更有利的条件.本节课的教学,从课堂实施的结果来看,由于不同的学生常常表现出不同的数学学习倾向,探究活动的过程和结果也不尽相同,教学中应当充分满足多样化的学习需求.本堂课以活动为载体,主要通过欣赏、操作、探究与设计等各种手段,充分体现学生的自主探索、合作交流和动手操作的学习方式,课堂把学习组织成了数学化的实践活动,让学生在课堂上看到了活生生的数学问题,感到数学与生活有密切联系,使学生真正领悟到数学的价值.在借助图形直观进行合情推理的过程中,学生能增强探究的好奇心,加深对数学的理解,激发出潜在的创造力,逐步形成创新意识.从设创情境到问题探究,具有趣味性,富有挑战性,.本节课采用的“主体建构模式”是让学生在解决问题中学,在动手实践中学.平面图形的密铺是体现多边形在现实生活中应用价值的一个方面,也是开发、培养学生创造性思维的一个重要渠道。本节课的设计就是使学生在“做中学”,真正体现了“以学生的发展为本”的宗旨.教师不是把新知识传授给学生,而是让学生去主动建构,但教师的引导和帮助对于学生的思考和知识的建构来说也是极为重要的.本节课创设了良好的学习环境去促进学生的学习,始终引导学生通过持续的观察、分折、猜想、概括、推证和验证等思维活动和学生的动手操作、交流讨论等活动,来建构起与此相关的知识经验.正象费赖登搭尔认为:数学知识既不是教出来的,也不是学出来的,而是研究出来的.而且在教学过程中不仅注意到要让学生掌握相应的数学知识,还感受到数学的实用价值,体会到数学来源于生活又为生活服务,我们学习的是有用的数学.
